Question

A cubic block weighing 1 kN and having sides 200 mm long is allowed to slide down an inclined plane, which has an angle of 300 with respect to the horizontal, on a film of oil having a thickness of 0.005 mm. Assuming a linear velocity profile across the oil layer, what is the terminal speed of the block

Answer 1

v = 1.49 m/s

Step-by-step explanation:

given,

side of block = 200 mm = 0.2 m

Terminal speed of the block

`v = (hWsin\theta)/(\mu\ A)`

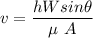
W is the weight of the block = 1 kN = 1000 N

h is the thickness of the = 0.005 mm

A is the area of the block

θ is the angle of inclination, = 30°

A = 6 a²

A = 6 x 0.2² = 0.24 m²

Viscosity of the oil,μ = 7 x 10⁻³N.s/m²

now, inserting all the values

`v = (0.005* 10^(-3)* 1000* \sin 30^(\circ))/(7* 10^(-3)* 0.24)`

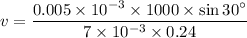
v = 1.49 m/s

Hence, the terminal velocity is equal to v = 1.49 m/s