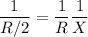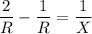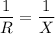Question

You have an RC timing circuit made from three capacitors, each C and in parallel with each other, and one resistor R. You wantto change the RC time constant to one-third what it was byremoving one of the capacitors and adding one resistor of theappropriate value. What does the new total resistance of theciruit need to be and how should you add the new resistor (seriesor parallel)

Answer 1

New total resistance = R/2

The new resistor is connected in parallel.

Step-by-step explanation:

Let
`T_1` be initial time constant and
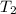`T_2` the new time constant.

The 3 capacitors are connected in parallel. The total capacitance,
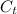`C_t`, is their sum. Hence

`C_t=C + C + C = 3C`

`T_1 = R * 3C = 3RC`

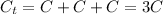
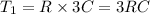
The new time constant is one-third of the initial time constant.

`T_2 = (T_1)/(3) = RC`

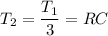
If one of the capacitors is removed, then the new total capacitance,
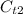`C_(t2)` is

`C_(t2) = 2C`

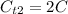
If the new total resistance isc
`R_(t2)`, then

`T_2 = R_(t2)C_(t2)`

`RC = R_(t2)*2C`

`R_(t2) = (R)/(2)`

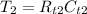
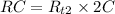
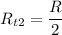
Since this is less than the old total resistance, the new resistor, with resistance, X, must be connected in parallel. Its value will be R, as below:

`(1)/(R/2)=(1)/(R)(1)/(X)`

`(2)/(R)-(1)/(R)=(1)/(X)`

`(1)/(R)=(1)/(X)`

`X = R`