Question

Consider the figure below. Abraham cut regular pentagon ABCDE into quadrilateral BEGC. Which of the following statements is true about quadrilateral BEGC? (picture included)

Answer 1

Correct: 2, 3, 4, 6

Explanation:

ABCDE is a regular pentagon. The sum of the measures of all interior angles in the pentagon is

`(n-2)\cdot 180^(\circ)=(5-2)\cdot 180^(\circ)=540^(\circ),`

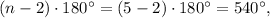
then the measure of each interior angles in the regular pentegon is

`(540^(\circ))/(5)=108^(\circ)`

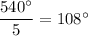
Triangle ABe is isosceles triangle, so the adjacent to the bas BE angle has the measure

`m\angle ABE=(180^(\circ)-108^(\circ))/(2)=36^(\circ)`

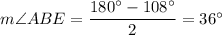
Therefore,

`m\angle CBE=m\angle ABC-m\angle ABE=108^(\circ)-36^(\circ)=72^(\circ)`

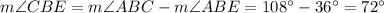
(option 2 is correct)

Since
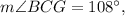`m\angle BCG=108^(\circ),` then

`m\angle EGC=108^(\circ )+4x`

The sum of the measures of all interior angles in quadrilateral BCGE is

`(n-2)\cdot 180^(\circ)=(4-2)\cdot 180^(\circ)=360^(\circ),`

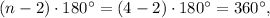
(option 6 is correct), then

`m\angle CBE+m\angle BEG+m\angle EGC+m\angle BCG=360^(\circ)\\ \\72^(\circ)+19x+3^(\circ)+108^(\circ)+4x+108^(\circ)=360^(\circ)\\ \\23x=69^(\circ)\\ \\x=3`

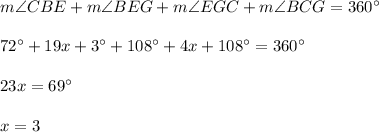
(option 1 is false)

`m\angle EGC=108^(\circ)+4\cdot 3^(\circ)=120^(\circ)`

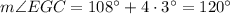
(option 3 is correct)

`m\angle GCB+m\angle EGC=108^(\circ)+72^(\circ)=180^(\circ)`

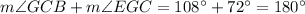
(option 4 is correct)

`m\angle BEC+m\angle EGC=(19\cdot 3+3+108+4\cdot 3)^(\circ)=180^(\circ)`

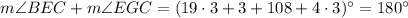
(option 5 is false)