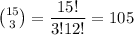Question

4. A circuit board uses three switches. We have three switches of type I, five of type II, and seven of type III. How many different choices are there?

Answer 1

105

Explanation:

On the assumption that each switch must be a different type, we need to choose 1 type I switch from 2, 1 type II switch from 5 and 1 type III switch from 7.

The number of ways of picking
`r` objects from
`n` objects is
`\binom{n}{r}=(n!)/(r!(n-r)!)`

`\binom{3}{1}=(3!)/(1!2!)=3`

`\binom{5}{1}=(5!)/(1!4!)=5`

`\binom{7}{1}= (7!)/(1!6!)=7`

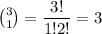
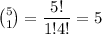
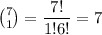
The total number of different choices =
`3*5*7=105`

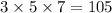
If there's no restriction on the choices, we would need to pick 3 socks from a total of 15.

`\binom{15}{3}=(15!)/(3!12!)=105`