Question

To haul a boat out of the water for the winter, a worker at the storage facility uses a wide strap with cables operating at the same angle (measured from the horizontal) on either side of the boat. Determine the tension in each cable if the boat has a mass of 510 kg and the angle of each cable is 46 ∘ from the horizontal and the boat is being momentarily held at rest. Compare this to the tension when the boat is raised and held at rest so the angle becomes 31 ∘.

Answer 1

Tension in each cable is 3474 N when angle made by the string with horizontal 46 degree

Tension in each cable is 4852 N when angle made by the string with horizontal 31 degree

Step-by-step explanation:

In this problem, for the boat to be at rest then tension in the strings must be such that the horizontal components balance each other and the vertical components balance weight of the boat.

Consider horizontal components for equilibrium

If the angle made by the string with horizontal 46 degree

`T_(1) cos\theta=T_(2) cos\theta\\T_(1)=T_{2`

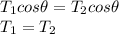
Tension the each string is same

Consider vertical components for equilibrium

`T_(1) sin\theta+T_(2) sin\theta=mg\\\\T_(1) sin46+T_(2) sin46=510 * 9.8\\\\2T_(1)sin46=4998............(here T_(1)=T_(2))\\T_(1)=3474.01 N`

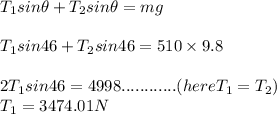
Tension in each cable is 3474 N when angle made by the string with horizontal 46 degree

If the angle made by the string with horizontal 31 degree, then

`T_(1) sin\theta+T_(2) sin\theta=mg\\\\T_(1) sin31+T_(2) sin31=510 * 9.8\\\\2T_(1)sin31=4998............(here T_(1)=T_(2))\\T_(1)=4852.06 N`

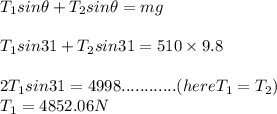
Tension in each cable is 4852 N when angle made by the string with horizontal 31 degree