Answer:
281.9 rolls
Step-by-step explanation:
Demand = D = 1450 rolls
Ordering cost = S = $15 per order
Holding cost = H = $3.42 x 16% = 0.5472 per unit per year
Economic order Quantity =
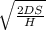
Economic order Quantity =

Economic order Quantity =
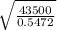
Economic order Quantity =
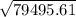
Economic order Quantity = 281.9 units
The Economic order quantity of the company is 281.9 units