Question

If the log↓b(a)=0, what is the value of a?
explain why log↓0 (3) and log↓1 (3) do not exist. ​

Answer 1

1. a = 1

2. See explanation below.

Explanation:

First Question

Given:

`\displaystyle \large{\log_b a = 0}`

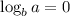
Convert to exponential:

`\displaystyle \large{\log_b a = c \to b^c = a}`

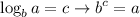
Thus
`\displaystyle \large{\log_b a = 0 \to b^0 = a}`

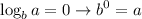
Evaluate:

`\displaystyle \large{b^0 = a}`

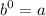
We know that for every values to power of 0 will always result in 1, excluding 0 to power of 0 itself.

Solution:

`\displaystyle \large{a = 1}`

__________________________________________________________

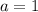
Second Question

Given:

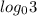`\displaystyle \large{log_0 3}` and
`\displaystyle \large{\log_1 3}`

Let’s convert to an equation:

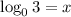`\displaystyle \large{\log_0 3 = x}` and
`\displaystyle \large{\log_1 3 = y}`

The variables represent unknown values of logarithm.

Convert to exponential:

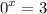`\displaystyle \large{0^x = 3}` and
`\displaystyle \large{1^y = 3}`

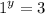
Notice that none of x-values and y-values will satisfy the equations. No matter what real numbers you put in, these equations will always be false.

Hence, no solutions for x and y.