Question

A researcher compares two compounds (1 and 2) used in the manufacture of car tires that are designed to reduce braking distances for SUVs equipped with the tires. SUVs equipped with tires using compound 1 have a mean braking distance of 69 feet and a standard deviation of 10.4 feet. SUVs equipped with tires using compound 2 have a mean braking distance of 71 feet and a standard deviation of 7.6 feet. Suppose that a sample of 81 braking tests are performed for each compound. Using these results, test the claim that the braking distance for SUVs equipped with tires using compound 1 is shorter than the braking distance when compound 2 is used. Let µ1 be the true mean braking distance corresponding to compound 1 and µ2 be the true mean braking distance corresponding to compound 2. Use the 0.05 level of significance.

Step 1 of 4: State the null and alternative hypotheses for the test.
Step 2 of 4: Compute the value of the test statistic. Round your answer to two decimal places.
Step 3 of 4: Determine the decision rule for rejecting the null hypothesis H0. Round the numerical portion of your answer to three decimal places.
Step 4 of 4: Make the decision for the hypothesis test.

Answer 1

Explanation:

Hello!

The objective of this experiment is to compare two compounds, designed to reduce braking distance, used in tire manufacturing to prove if the braking distance of SUV's equipped with tires made with compound 1 is shorter than the braking distance of SUV's equipped with tires made with compound 2.

So you have 2 independent populations, SUV's equipped with tires made using compound 1 and SUV's equipped with tires made using compound 2.

Two samples of 81 braking tests are made and the braking distance was measured each time, the study variables are determined as:

X₁: Braking distance of an SUV equipped with tires made with compound one.

Its sample mean is X[bar]₁= 69 feet

And the Standard deviation S₁= 10.4 feet

X₂: Braking distance of an SUV equipped with tires made with compound two.

Its sample mean is X[bar]₂= 71 feet

And the Standard deviation S₂= 7.6 feet

We don't have any information on the distribution of the study variables, nor the sample data to test it, but since both sample sizes are large enough n₁ and n₂ ≥ 30 we can apply the central limit theorem and approximate the distribution of both variables sample means to normal.

The researcher's hypothesis, as mentioned before, is that the braking distance using compound one is less than the distance obtained using compound 2, symbolically: μ₁ < μ₂

The statistical hypotheses are:

H₀: μ₁ ≥ μ₂

H₁: μ₁ < μ₂

α: 0.05

The statistic to use to compare these two populations is a pooled Z test

Z= (X[bar]₁-X[bar]₂) - (μ₁ - μ₂) ≈ N(0;1)

`\sqrt{(S^2_1)/(n_1)+(S^2_2)/(n_2) }`

`Z= \frac{(69 - 71) - 0}{\sqrt{(108.16)/(81) + (57.76)/(81) } } = (-2)/(1.43) = -1.397`

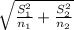
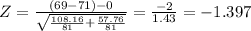
The rejection region if this hypothesis test is one-tailed to the right, so you'll reject the null hypothesis to small values of the statistic. The critical value for this test is:

`Z{\alpha }= Z_(0.05) = -1.648`

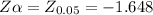
Decision rule:

If
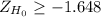`Z_(H_0) \geq -1.648`, then you do not reject the null hypothesis.

If
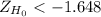`Z_(H_0) < -1.648`, then you reject the null hypothesis.

Since the statistic value is greater than the critical value, the decision is to not reject the null hypothesis.

At a 5% significance level, you can conclude that the average braking distance of SUV's equipped with tires manufactured used compound 1 is greater than the average braking distance of SUV's equipped with tires manufactured used compound 2.

I hope it helps!