Question

. Determine whether the vectors (5, −2, 4), (2, −3, 5), and (4, 5−

7) are linearly independent or dependent.

Answer 1

The vectors are linearly independent

Explanation:

These vectors can be written in a matrix form as:

`\left[\begin{array}{ccc}5&-2&4\\2&-3&5\\4&5&-7\end{array}\right]`

and if the matrix is invertible, the system has a unique solution, and hence, the vectors that form the matrix are linearly independent.

A matrix is invertible if it's determinant is different from zero.

Suppose A is a matrix, A is invertible if |A| ≠ 0

`\left|\begin{array}{ccc}5&-2&4\\2&-3&5\\4&5&-7\end{array}\right| \\`

=
`5\left|\begin{array}{cc}-3&5\\5&-7\end{array}\right| - (-2)\left|\begin{array}{cc}2&5\\4&-7\end{array}\right| + 4\left|\begin{array}{cc}2&-3\\4&5\end{array}\right|`

=
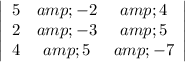
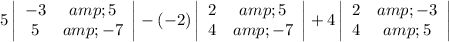
`= 5[-7(-3) - 5(5)] + 2[2(-7) - 4(5)] + 4[5(2) - 4(-3)]\\= 5(21 - 25) + 2( -14 -20) + 4(10 + 12)\\= 5(-4) + 2(-34) + 4(21)\\= -20 - 68 + 84\\= -4\\`

Since this is not zero, we conclude that the vectors are linearly independent.

Answer 2

Answer: The vectors are linearly dependent.

The solution is in the attachment