Question

Wire A and wire B are made from the same material and are under the same tension, but waves travel along string B at one-third the wave speed of string A. The radius of wire A is 0.100 mm. What is the radius of wire B

Answer 1

0.3 mm

Step-by-step explanation:

`\rho` = Density of material

`\mu` = Linear density of the material =
`\rho A`

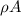
Area = Area =
`\pi r^2`

r = Radius

The velocity of a wave is given by

`v=\sqrt{(T)/(\mu)}\\\Rightarrow v=\sqrt{(T)/(\rho A)}\\\Rightarrow v=\sqrt{(T)/(\rho \pi r^2)}`

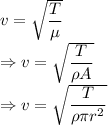
It can be seen that the velocity is inversly proportional to the radius

`v\propto \sqrt{(1)/(r^2)}\\\Rightarrow v\propto (1)/(r)`

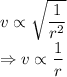
So,

`(v_a)/(v_b)=(r_b)/(r_a)`

From the question

`v_b=(1)/(3)v_a`

`\\\Rightarrow (v_a)/((1)/(3)v_a)=(r_b)/(0.1)\\\Rightarrow 3=(r_b)/(0.1)\\\Rightarrow r_b=3* 0.1\\\Rightarrow r_b=0.3\ mm`

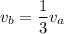
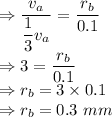
The radius of wire B is 0.3 mm