Answer:
 = 19
= 19
ΔG° of the reaction forming glucose 6-phosphate = -7295.06 J
ΔG° of the reaction under cellular conditions = 10817.46 J
Step-by-step explanation:
Glucose 1-phosphate ⇄ Glucose 6-phosphate
Given that: at equilibrium, 95% glucose 6-phospate is present, that implies that we 5% for glucose 1-phosphate
So, the equilibrium constant
 can be calculated as:
can be calculated as:

![= ([glucose-6-phosphate])/([glucose-1-[phosphate])](https://img.qammunity.org/2021/formulas/chemistry/college/xmytripinesvxv7sc671owy67m7ssdkxzq.png)


 = 19
= 19
The formula for calculating ΔG° is shown below as:
ΔG° = - RTinK
ΔG° = - (8.314 Jmol⁻¹ k⁻¹ × 298 k × 1n(19))
ΔG° = 7295.05957 J
ΔG°≅ - 7295.06 J
b)
Given that; the concentration for glucose 1-phosphate = 1.090 x 10⁻² M
the concentration of glucose 6-phosphate is 1.395 x 10⁻⁴ M
Equilibrium constant
 can be calculated as:
can be calculated as:

![= ([glucose-6-phosphate])/([glucose-1-[phosphate])](https://img.qammunity.org/2021/formulas/chemistry/college/xmytripinesvxv7sc671owy67m7ssdkxzq.png)
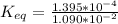
 0.01279816514 M
0.01279816514 M
 0.0127 M
0.0127 M
ΔG° = - RTinK
ΔG° = -(8.314*298*In(0.0127)
ΔG° = 10817.45913 J
ΔG° = 10817.46 J