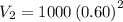Question

You buy a car for 1000 every year it loses 40% of its value

Write an explicit equation that represents this situation.
How much would the car be worth after 2 years?

Answer 1

`\displaystyle V_n=V_o\left(0.60\right)^n`

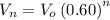
The car is worth 360 after two years

Explanation:

Model For Depretiation

Assume the situation of something that has an initial value Vo and loses its value by a x% every year. The first year it will lose

`\displaystyle (xV_o)/(100)`

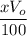
and it will have a new value of

`\displaystyle V_1=V_o-x(V_o)/(100)=V_o\left((100-x)/(100)\right)`

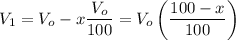
Next year it will have a value of

`\displaystyle V_2=V_o\left((100-x)/(100)\right)^2`

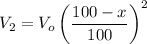
Since x=40%, we can deduct the general formula

`\displaystyle V_n=V_o\left(0.60\right)^n`

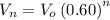
For n=2

`\displaystyle V_2=1000\left(0.60\right)^2`

`V_2=360`