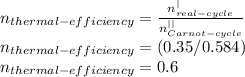Question

A real (non-Carnot) heat engine, operating between heat reservoirs at temperatures of 650 K and 270 K, performs 4.3 kJ of net work and rejects 8.0 kJ of heat in a single cycle. What is the thermal efficiency of this heat engine?

Answer 1

`n_(thermal-efficiency)=0.6`

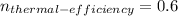
Step-by-step explanation:

Given data

Temperature T1=270K

Temperature T2=650K

Work=4.3 kJ

Heat rejects=8.0 kJ

To find

Thermal efficiency

Solution

The thermal efficiency is given as:

`n_(thermal-efficiency)=(n^(|)_(real-cycle) )/(n^(||)_(Carnot-cycle) )`

For Carnot cycle efficiency

`n^(||)=1-(T1/T2)\\n^(||)=1-(270K/650K)\\n^(||)=0.584\\`

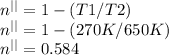
For real cycle efficiency

`n^(|)=(4.3)/(4.3+8.0)\\n^(|)=0.35\\`

So the thermal efficiency is:

`n_(thermal-efficiency)=(n^(|)_(real-cycle) )/(n^(||)_(Carnot-cycle) )\\n_(thermal-efficiency)=(0.35/0.584)\\ n_(thermal-efficiency)=0.6`