Question

A particle, originally at rest and located at point (3 ft, 2 ft, 5 ft), is subjected to an acceleration of a = 56t i + 12 t 2k6 ft>s2. Determine the particle’s position (x, y, z) at t = 1 s.

Answer 1

What I understand that acceleration a={56ti+12t²k}ft/s²

Answer:

The particle position is (12.333 ft, 2 ft, 6 ft )

Step-by-step explanation:

Given data

Particle located at point (3 ft, 2 ft,5 ft)

Acceleration a={56ti+12t²k}ft/s²

To find

Particle position

Solution

As given acceleration is

`\int\limits^(v)_(o) \, dv=\int\limits^(t)_(o) {56ti+12t^(2)k } \, dt\\ v=28t^(2) i+4t^(3)k\\\int\limits^(r)_{r_(o) } {} \, dr=\int\limits^(t)_(o) {28t^(2) i+4t^(3)k} \, dt\\ r-r_(o)=9.333t^(3)i+t^(4)k\\`

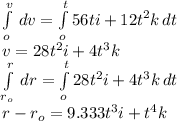
r₀ is given as=(3i+2j+5k)

So

`r-r_(o)=9.333t^(3)i+t^(4)k\\r-(3i+2j+5k)=9.333t^(3)i+t^(4)k\\at\\t=1s\\r-(3i+2j+5k)=9.333(1)^(3)i+(1)^(4)k\\r-(3i+2j+5k)=9.333i+k\\r=9.333i+k+(3i+2j+5k)\\r=12.333i+2j+6k\\`

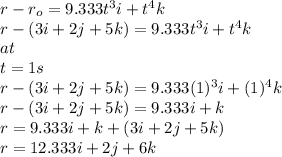
So the particle position is (12.333 ft, 2 ft, 6 ft )