What I understand that acceleration a={56ti+12t²k}ft/s²
Answer:
The particle position is (12.333 ft, 2 ft, 6 ft )
Step-by-step explanation:
Given data
Particle located at point (3 ft, 2 ft,5 ft)
Acceleration a={56ti+12t²k}ft/s²
To find
Particle position
Solution
As given acceleration is
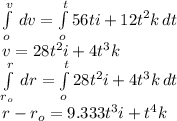
r₀ is given as=(3i+2j+5k)
So
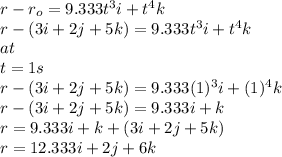
So the particle position is (12.333 ft, 2 ft, 6 ft )