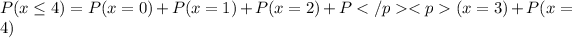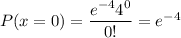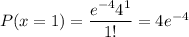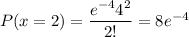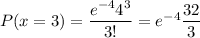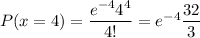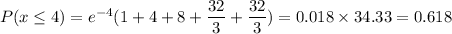Answer:
0.618
Explanation:
This is a binomial distribution. We are to determine the probability of people unsatisfied. If we denote the probability of being satisfied with
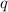 , then
, then
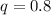 . Let
. Let
 be the probability of being unsatisfied. Then
be the probability of being unsatisfied. Then
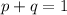
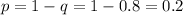
Since the random sample is 20 and
 is small enough, we can use the Poisson probability function
is small enough, we can use the Poisson probability function
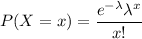
where
 is the mean and is given by
is the mean and is given by
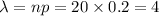 .
.
Denoting the probability of at most 4 unsatisfied with
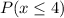 ,
,