Question

A personnel manager is concerned about absenteeism. She decides to sample employee records to determine if absenteeism is distributed evenly throughout the six-day workweek. The null hypothesis is: Absenteeism is distributed evenly throughout the week. The 0.01 level is to be used. The sample results are: Day of the Week Number of Employees Absent Monday 12 Tuesday 9 Wednesday 11 Thursday 10 Friday 9 Saturday 9 What is the critical value of chi-square with α = 0.05? Select one: a. 11.070 b. 12.592 c. 13.388 d. 15.033

Answer 1

`df=categor-1=6-1=5`

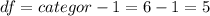
The critical value can be founded with the following Excel formula:

=CHISQ.INV(1-0.05,5)

And we got
`\chi^2_(critc)= 11.0705`

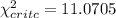
a. 11.070

And since our calculated value is lower than the critical we FAIL to reject the null hypothesis at 5% of significance

Explanation:

Previous concepts

A chi-square goodness of fit test "determines if a sample data matches a population".

A chi-square test for independence "compares two variables in a contingency table to see if they are related. In a more general sense, it tests to see whether distributions of categorical variables differ from each another".

Solution to the problem

For this case we want to test:

H0: Absenteeism is distributed evenly throughout the week

H1: Absenteeism is NOT distributed evenly throughout the week

We have the following data:

Monday Tuesday Wednesday Thursday Friday Saturday Total

12 9 11 10 9 9 60

The level of significance assumed for this case is
`\alpha=0.05`

The statistic to check the hypothesis is given by:

`\sum_(i=1)^n ((O_i -E_i)^2)/(E_i)`

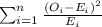
The table given represent the observed values, we just need to calculate the expected values with the following formula
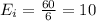`E_i = (60)/(6)= 10` and the expected value is the same for all the days since that's what we want to test.

now we can calculate the statistic:

`\chi^2 = ((12-10)^2)/(10)+((9-10)^2)/(10)+((11-10)^2)/(10)+((10-10)^2)/(10)+((9-10)^2)/(10)+((9-10)^2)/(10)=0.8`

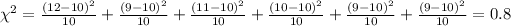
Now we can calculate the degrees of freedom (We know that we have 6 categories since we have information for 6 different days) for the statistic given by:

`df=categor-1=6-1=5`

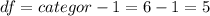
The critical value can be founded with the following Excel formula:

=CHISQ.INV(1-0.05,5)

And we got
`\chi^2_(critc)= 11.0705`

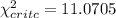
a. 11.070

And since our calculated value is lower than the critical we FAIL to reject the null hypothesis at 5% of significance