Question

Ask Your Teacher A tank contains 350 liters of fluid in which 10 grams of salt is dissolved. Pure water is then pumped into the tank at a rate of 5 L/min; the well-mixed solution is pumped out at the same rate. Find the number A(t) of grams of salt in the tank at time t.

Answer 1

`A=10e^{(-t)/(350) }`

Explanation:

Given that a tank contains 350 liters of fluid in which 10 grams of salt is dissolved. Pure water is then pumped into the tank at a rate of 5 L/min

the well-mixed solution is pumped out at the same rate.

Let A(t) be the grams of salt at time t.

Then A(0) = 10 gm

Inflow of fluid = outflow of fluid = 5l/min

So volume of tank at time t = 350 litres

Rate of change of salt = A'(t) = incoming rate - outgoing rate

= 0-
`A(t)/350`

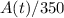
i.e.
`(dA)/(dt) =(-A)/(350) \\ln A = -t/350 +C\\A = Pe^{(-t)/(350) }`

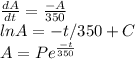
Use the fact that when t =0, A = 10

P = 10

So we get

`A=10e^{(-t)/(350) }`