Question

A recent study of the relationship between social activity and education for a sample of corporate executives showed the following results. Social Activity Education Above Average Average Below Average College 30 20 10 High School 20 40 90 Grade School 10 50 130 Based on the analysis, what can be concluded? Select one: a. Social activity and education are correlated. b. Social activity and education are not related. c. Social activity and education are related. d. No conclusion is possible.

Answer 1

c. Social activity and education are related.

Explanation:

Hello!

You have two categorical variables

X₁: Social activity of an individual (Categorized: Above average, aAverage, Below Average)

X₂: Educational level of an individual (Categorized: College, High School and Grade School)

You need to test if this two variables are or nor related, in other words, if they are independent. The propper statistic analysis to test it is a Chis Square tesr for independence. So the hypotheses are:

H₀:
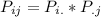`P_(ij)= P_(i.) * P_(.j)` ∀ i= 1, 2, 3 and j= 1, 2, 3

H₁: The variables are not independent.

α: 0.05

The statistic is:

`X^2= EE((o_(ij)-e_(ij))^2)/(e_(ij)) ~X^2_((r-1)(c-1))`

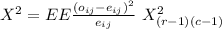
Where

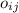`o_(ij)` is the observed frequency for ij categories

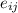`e_(ij)` is the expected frequency for the ij categories

r= total of rows

c= total of columns

The rejection region of this test is always one-tailed to the right so the critical value and decision rule are:

`X^2_((r-1)(c-1);1-\alpha )= X^2_((3-1)(3-1);1-0.05) = X^2_(4;0.95)= 9.488`

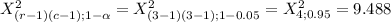
If
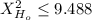`X^2_(H_o) \leq 9.488` you do not reject the null hypothesis.

If
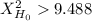`X^2_(H_0) > 9.488` you reject the null hypothesis.

To calculate the statistic you need to calculate the expected frequencies for all categories using the following formula:

`e_(ij)= (O_(i.)*O_(.j))/(n)`

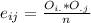
Where

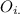`O_(i.)` is the total observed frequency of the i-row

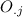`O_(.j)` is the total observed frequency of the j-column

So for example the expected frequency for the first row and first column is:

`e_(11)= (O_(1.)*O_(.1))/(n) = (60*60)/(400)= 9`

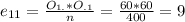
And so on:

`e_(12)= (O_(1.)*O_(.2))/(n)= (60*110)/(400)= 16.5`

`e_(13)= (O_(1.)*O_(.3))/(n)= (60*230)/(400)= 34.5`

`e_(21)= (O_(2.)*O_(.1))/(n)= (150*60)/(400)= 22.5`

`e_(22)= (O_(2.)*O_(.2))/(n)= (150*110)/(400)= 41.25`

`e_(23)= (O_(2.)*O_(.3))/(n)= (150*230)/(400)= 86.25`

`e_(31)= (O_(3.)*O_(.1))/(n)= (190*60)/(400)= 28.5`

`e_(32)= (O_(3.)*O_(.2))/(n)= (190*110)/(400)= 52.25`

`e_(33)= (O_(3.)*O_(.3))/(n)= (190*230)/(400)= 109.25`

`X^2_(H0)= ((30-9)^2)/(9)+ ((20-16.5)^2)/(16.5)+ ((10-34.5)^2)/(34.5) + (...)`

`X^2_(H_0)= 96.99`

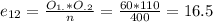
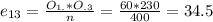
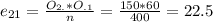
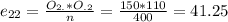
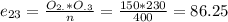
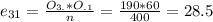
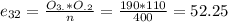
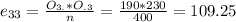
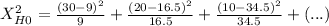
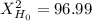
The decision is to reject hte null hypothesis, the two variables are dependant.

I hope it helps!