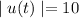Question

Consider the initial value problem

4u'' − u' + 2u = 0, u(0) = 3, u'(0) = 0.
(a) Find the solution u(t) of this problem.
(b) For t > 0, find the first time at which |u(t)| = 10. Round your answer to four decimal places.

Answer 1

Answer with Step-by-step explanation:

We are given that initial value problem

a.
`4u''-u'+2u=0`

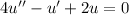
u(0)=3,u'(0)=0

Auxillary equation

`4m^2-m+2=0`

`m=(1\pm√((-1)^2-4(4)(2)))/(2(4))`

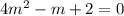
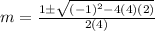
By using quadratic formula:
`x=(-b\pm√(b^2-4ac))/(2a)`

`m=(1\pm√(1-32))/(8)`

`m=(1\pm i√(31))/(8)=(1)/(8)\pm i(√(31))/(8)`

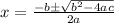
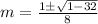
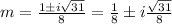
Therefore, the general solution of the initial value problem

`u(t)=e^{(t)/(8)}(c_1cos(√(31))/(8)t+c_2sin(√(31))/(8)t)`

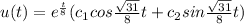
Substitute t=0 and u(0)=3

`3=c_1`

Differentiate w.r.t t

`u'(t)=(1)/(8)e^{(t)/(8)}(c_1cos(√(31))/(8)t+c_2sin(√(31))/(8)t)+e^{(t)/(8)}(-(√(31))/(8)c_1sin(√(31))/(8)t+(√(31))/(8)c_2cos(√(31))/(8)t)`

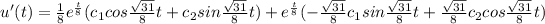
Substitute t=0 and u'(0)=0

`0=(1)/(8)c_1+(√(31))/(8)c_2`

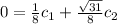
Substitute the value of
`c_1`

`0=(1)/(8)* 3+(√(31))/(8)c_2`

`-(3)/(8)=(√(31))/(8)c_2`

`c_2=-(3)/(8)* (8)/(√(31))`

`c_2=-(3)/(√(31))`

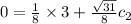
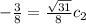
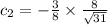
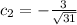
Substitute the values

`u(t)=e^{(t)/(8)}(3cos(√(31))/(8)t-(3)/(√(31))sin(√(31))/(8)t)`

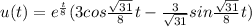
(b) For t>0
`\mid u(t)\mid=10`

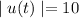
We cannot find the solution of
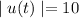`\mid u(t)\mid=10`analytically

But we can use the graph to find the approximate value of the solution.

By graph , the approximate value of t=12.2 for which
`\mid u(t)\mid=10`