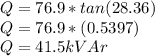Question

At full load, a commercially available 100hp, three phase induction motor operates at an efficiency of 97% and a power factor of 0.88 lag. The motor is supplied from a three-phase outlet with a line voltage rating of 208V.a. What is the magnitude of the line current drawn from the 208 V outlet? (1 hp = 746 W.) b. Calculate the reactive power supplied to the motor.

Answer 1

I = Line Current = 242.58 A

Q = Reactive Power = 41.5 kVAr

Step-by-step explanation:

Firstly, converting 100 hp to kW.

Since, 1 hp = 0.746 kW,

100 hp = 0.746 kW x 100

100 hp = 74.6 kW

The power of a three phase induction motor can be given as:

`P_(in) = √(3) VI Cos\alpha\\`

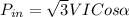
where,

P in = Input Power required by the motor

V = Line Voltage

I = Line Current

Cosα = Power Factor

Now, calculating Pin:

`efficiency = \frac{{P_(out)} }{P_(in) }\\0.97 = (74.6)/(P_(in) ) \\P_(in) = (74.6)/(0.97)\\ P_(in) = 76.9 kW`

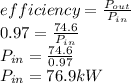
a) Calculating the line current:

`P_(in) = √(3)VICos\alpha \\76.9 * 1000= √(3)*208*I*0.88\\I = (76.9*1000)/(√(3)*208*0.88 )\\I = 242.58 A`

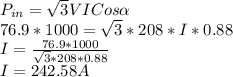
b) Calculating Reactive Power:

The reactive power can be calculated as:

Q = P tanα

where,

Q = Reactive power

P = Active Power

α = power factor angle

Since,

`Cos\alpha =0.88\\\alpha =Cos^(-1)(0.88)\\\alpha=28.36`

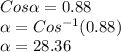
Therefore,

`Q = 76.9 * tan (28.36)\\Q = 76.9 * (0.5397)\\Q = 41. 5 kVAr`