Answer:
6.68% or 0.0668
Explanation:
Mean sheet length (μ) = 30.05 inches
Standard deviation (σ) = 0.2 inches
In a normal distribution, for any length X, the z-score is determined by the following expression:
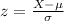
For X = 29.75, the z-score is:
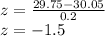
A z-score of -1.5 corresponds to the 6.68th percentile of a normal distribution.
Therefore, the probability that a sheet selected at random will be less than 29.75 inches long is 6.68%.