Answer:
The difference in thickness is 56.32 nm.
Step-by-step explanation:
Given that,
Wavelength = 700 nm
Refractive index = 1.33
The constructive interference of light reflecting from the top of thin film
Using formula for constructive interference
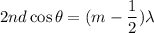
Where, d = thickness of film
n = refractive index of film
 = wave length of incident light
= wave length of incident light
Here, m= 1,2,3....
For the longest interference, m = 1
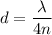
We need to calculate the distance
Put the value into the formula of distance
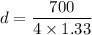
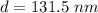
(b). Now, wavelength = 400 nm
We need to calculate the distance for same order
Again put the value into the formula of distance
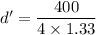
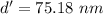
We need to calculate the difference in thickness
Using formula of thickness
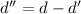
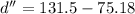
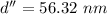
Hence, The difference in thickness is 56.32 nm.