Answer:
Explanation:
Given that a young person with no initial capital invests k dollars per year at an annual rate of return r. Assume that investments are made continuously and that the return is compounded continuously
a) Amount accumulated at time t
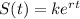 , where r = rate of interest and t = time lapsed
, where r = rate of interest and t = time lapsed
b) Here S = 1,000,000
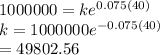
So 49802.56 dollars to be invested to get 1 million after 40 years
c) k = 2000 per year
I 2000 will be for 40 years, II 2000 for 39 years, ..... Last 2000 for 0 years
i.e. final amount would be
![2000[(e^(40r) +(e^(39r) +....e^r] = 1000000\\500 = (e^r(e^(40r)-1)/(e^r-1)](https://img.qammunity.org/2021/formulas/mathematics/high-school/p2c7d7n26mhj5233n4vy0uyvjzsouuadih.png)
solving we get r = 9.6% approxy