Question

Calculate the ratio of the drag force on a passenger jet flying with a speed of 950 km/h at an altitude of 10 km to the drag force on a prop-driven transport flying at one-fifth the speed and half the altitude of the jet. At 10 km the density of air is 0.38 kg/m3 and at 5.0 km it is 0.67 kg/m3. Assume that the airplanes have the same effective cross-sectional area and the same drag coefficient C.

Answer 1

14.18

Step-by-step explanation:

given,

Speed of passenger jet,v₁ = 950 Km/h

Altitude of flight, h₁ = 10 km

Prop-driven speed,v₂ = 950/5 = 190 Km/h

altitude,h₂ = 5 Km

density of air at 10 Km = 0.38 Kg/m³

density of air at 5 Km = 0.67 Kg/m³

Drag force formula

`F = (1)/(2)C\rho Av^2`

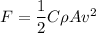
now, ratio of drag Force

`(F_(jet))/(F_(prop))=((1)/(2)C\rho_(10) Av_(1)^2)/((1)/(2)C\rho_(5) Av_2^2)`

`(F_(jet))/(F_(prop))=(\rho_(10) v_(1)^2)/(\rho_(5)v_2^2)`

`(F_(jet))/(F_(prop))=(0.38* 950^2)/(0.67* 190^2)`

`(F_(jet))/(F_(prop))=14.18`

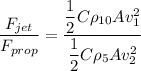
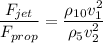
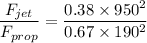
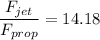
Hence, the ration of the drag force is equal to 14.18.