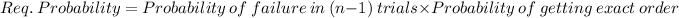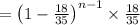Question

(Ross, 4.78) A jar contains 4 white and 4 black marbles. We randomly choose 4 marbles. If 2 of them are white and 2 are black, we stop. If not, we replace the marbles in the jar and again randomly select 4 marbles. This continues until exactly 2 of the 4 chosen are white. What is the probability that we shall make exactly n selections?

Answer 1

Explanation:

Given

Jar contains 4 white and 4 black marbles

We randomly select 4 marbles out of which 2 are white and 2 are black

Probability that 2 white and 2 black marbles are selected is

`P=(^4C_2* ^4C_2)/(^8C_4)`

`P=(18)/(35)`

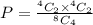
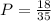
The process is continue for n trails until we choose the correct order

i.e. we have to fail in n-1 trails

For exact n selection Probability is given by

`Req.\ Probability=Probability\ of\ failure\ in\ (n-1)\ trials* Probability\ of\ getting\ exact\ order`

`=\left ( 1-(18)/(35)\right )^(n-1)* (18)/(35)`