Question

Consider a population in which 80% of males and 60% of females are employed. In this population, 55% of individuals are females. If I pick five persons at random from this population, what is the probability that no more than one of those chosen is not employed?

Answer 1

The probability that no more than 1 person is not employed is 0.5077.

Explanation:

Let's denote the events as:

E = a person is employed

M = a person is male

F = a person is a female.

Given:

P (E | M) = 0.80

P (E | F) = 0.60

P (F) = 0.55

P (M) = 1 - P (F) = 1 - 0.55 = 0.45

Compute the probability that a randomly selected person is employed as follows

P (E) = P (E | M) × P (M) + P (E | F) × P (F)

`=(0.80*0.45)+(0.60*0.55)\\=0.69`

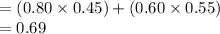
Then the probability that a randomly selected person is not employed is,

P (E') = 1 - P (E) = 1 - 0.69 = 0.31

Now let's assume X = number of employees that are not employed.

The sample selected is of size, n = 5.

Then the random variable
`X\sim Bin(n=5, p=0.31)`

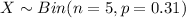
The probability function of Binomial distribution is:

`P(X=x)={n\choose x}p^(x)(1-p)^(n-x)`

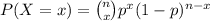
Compute the probability that no more than 1 person is not employed as follows:

P (X ≤ 1) = P (X = 0) - P (X = 1)

`={5\choose 0}(0.31)^(0)(1-0.31)^(5-0)+{5\choose 1}(0.31)^(1)(1-0.31)^(5-1)\\=0.1564-0.3513\\=0.5077`

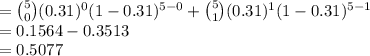
Thus, the probability that no more than 1 person is not employed is 0.5077.