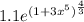Answer:
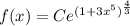
The explicit solution of the initial value problem=y=
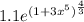
Explanation:
We are given that first order separable equation
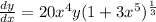
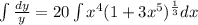
Suppose
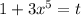
Differentiate w.r.t x
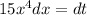
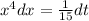
Substitute the values
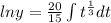
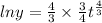 +C
+C
By using the formula
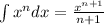 +C
+C
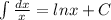
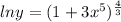 +C
+C
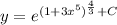
By using identity :
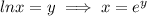
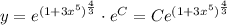
By using identity :
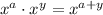
Where
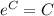
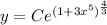
By compare with y=Cf(x)
We get
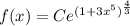
We are given that y(0)=3
Substitute the value
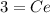
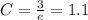
Substitute the value
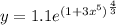
The explicit solution of the initial value problem=y=