Question

Two basketball players are essentially equal in all respects. (They are the same height, they jump with the same initial velocity, etc.) In particular, by jumping they can raise their centers of mass the same vertical distance, H (called their "vertical leap"). The first player, Arabella, wishes to shoot over the second player, Boris, and for this she needs to be as high above Boris as possible. Arabella jumps at time ?

Answer 1

Two basketball players are essentially equal in all respects.(They are the same height, they jump with the same initial velocity, etc.) In particular, by jumping they can raise their centers of mass the same vertical distance, H (called their "vertical leap"). The first player,Arabella, wishes to shoot over the second player, Boris, and forth is she needs to be as high above Boris as possible. Arabella jumps at time t = 0, and Boris jumps later, at time
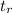`t_(r)` (his reaction time). Assume that Arabella has not yet reached her maximum height when Boris jumps.

Part A.) Find the vertical displacement D(t) =
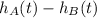`h_(A) (t) - h_(B)(t)`, as a function of time for the interval 0 < t <
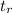`t_(r)` , where
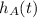`h_(A) (t)` is the height of the raised hands of Arabella, while
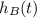`h_(B)(t)` is the height of the raised hands of Boris. (Express thevertical displacement in terms of H, g,and t.)

Part B.) Find the vertical displacement D(t) between the raised hands of the two players for the time period after Boris has jumped (t >
`t_(R)` ) but before Arabella has landed. (Express your answer in terms of t,
`t_(R)`, g, and H)

Part C.) What advice would you give Arabellato minimize the chance of her shot being blocked?

Shoot when you have the maximum vertical velocity.

Shoot at the instant Boris leaves the ground.

Shoot when you have the same vertical velocity as Boris.

Shoot when you reach the top of your jump (when your height is ).

The answers to the question are

a) √(2×g×H) ×t -0.5×g×t²

b) (√(2×g×H)+ 0.5× (
`t_(R)` -t) ×g) ×
`t_(R)`

c) Shoot at the instant Boris leaves the ground

Step-by-step explanation:

For Arabella
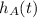`h_(A) (t)` = h₀ + v₀×t - 0.5×g×t²

Height of Boris =
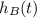`h_(B)(t)` = h₀ + v₀×(t-
`t_(R)`) - 0.5×g×(t-
`t_(R)`)²

During the period 0 < t <
`t_(r)`,
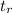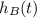`h_(B)(t)` = h₀

Hence D(t) =
`h_(A) (t) - h_(B)(t)` =
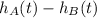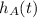`h_(A) (t)` = h₀ + v₀×t - 0.5×g×t² - h₀

= v₀×t - 0.5×g×t² = √(2×g×H) ×t -0.5×g×t²

b) for t >
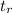`t_(r)` we have

D(t) =
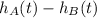`h_(A) (t) - h_(B)(t)` = h₀ + v₀×t - 0.5×g×t² - (h₀ + v₀×(t-
`t_(R)`) - 0.5×g×(t-
`t_(R)`)²)

=v₀×t - 0.5×g×t² - v₀×(t-
`t_(R)`) + 0.5×g×(t-
`t_(R)`)²

=v₀×
`t_(R)` - 0.5×g×t² +0.5×g×(t²-2×t×
`t_(R)` +
`t_(R)`²)

= v₀×
`t_(R)` +0.5×g×
`t_(R)` ²-g×t×
`t_(R)`

=√(2×g×H)×(
`t_(R)` ) + 0.5×g×
`t_(R)` ²-g×t×
`t_(R)`

= √(2×g×H)×(
`t_(R)` ) + 0.5× (
`t_(R)` -t) g×
`t_(R)`

(√(2×g×H)+ 0.5× (
`t_(R)` -t) ×g) ×
`t_(R)`

(c) From the the above equation we get by differentiating

d((√(2×g×H)+ 0.5× (
`t_(R)` -t) ×g) ×
`t_(R)` )/dtr

= √(2×g×H) + g×(
`t_(R)` - t) and since t >
`t_(R)` then D(t) =
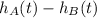`h_(A) (t) - h_(B)(t)` will be highest when
`t_(R)` = 0

Shoot at the instant Boris leaves the ground