Question

A sphere of radius R = 0.295 m and uniform charge density -151 nC/m^3 lies at the center of a spherical, conducting shell of inner and outer radii 3.50 R and 4.00 R , respectively. If the conducting shell carries a total charge of Q = 66.7nC , find the magnitude of the electric field at the at the following radial distances from the center of the charge distribution.

a. 0.760R
b. 3.90R
c. 2.80R
d. 7.30R

Answer 1

To determine the electric field at different radial distances from a charged sphere and a concentric conducting shell, Gauss's Law is used, which involves the enclosed charge and the permittivity of free space.

Step-by-step explanation:

To find the magnitude of the electric field at various radial distances from the center of a charge distribution involving a sphere with a uniform charge density and a concentric spherical conducting shell with given inner and outer radii, we can use Gauss's Law. Gauss's Law states that the electric field times the area of a Gaussian surface is equal to the enclosed charge divided by the permittivity of free space (ε0).

• 
  
• At 0.760R, we are inside the uniformly charged sphere. The enclosed charge is determined by the volume up to that radius and the charge density.
• 
  
• At 3.90R, we are outside the outer radius of the conducting shell, so the electric field is that due to the total charge on the shell plus the sphere, spread out over the surface of a sphere of radius 3.90R.
• 
  
• At 2.80R, we are inside the conducting shell but outside the uniformly charged sphere. The electric field here is due only to the charge of the inner sphere.
• 
  
• At 7.30R, similar to part b, we are outside both the sphere and the shell, and the electric field calculation follows the same principle as in part b.

It is essential to remember that the electric field inside a conductor in electrostatic equilibrium is zero, and any excess charge resides on the surface.

Answer 2

a) -1.27*10³ N/C b) 0 c) -0.21*10³ N/C d) 0.1*10³ N/C

Step-by-step explanation:

a) r = 0.76R

As this distance is inside the sphere, we need to know how much charge is enclosed within this distance for the center, as follows:

Q = ρ*V(r) = ρ*
`(4)/(3) *\pi *r^(3)`

where r = 0.760* R = 0.760* 0.295 m = 0.224 m, and ρ = -151 nC/m³

`Q = -151e-9 *(4)/(3) *\pi *0.224m^(3) = -7.11e-9 C`

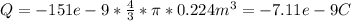
Applying Gauss' Law to a spherical gaussian surface of r= 0.76R, as the electric field is radial, and directed inward, we can write the following equation:

E*A = Q/ε₀, where Q= -7.11 nC, A= 4*π*(0.76R)² and ε₀ =8.85*10⁻¹² C²/N*m²

We can solve for E, as follows:

`E = (1)/(4*\pi*8.85e-12C2/N*m2 ) *(-7.11e-9C)/((0.76*0.295m)^(2)) =-1.27e3 N/C`

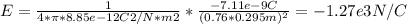
⇒ E = -1.27*10³ N/C

b) r= 3.90 R

As this distance falls inside the conducting shell, and no electric field can exist within a conductor in electrostatic condition, E=0

c) r = 2.8 R

As this distance falls between the sphere and the inner radius of the shell, we can calculate the electric field, applying Gauss' law to a gaussian surface of radius equal to r= 2.80 R.

First we need to find the total charge of the sphere, as follows:

Q = ρ*V =

`Q = -151e-9 *(4)/(3) *\pi *0.295m^(3) = -16.2e-9 C`

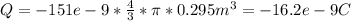
In the same way that for a) we can write the following expression:

E*A = Q/ε₀, where Q= -16.2 nC, A= 4*π*(2.8R)² and ε₀ =8.85*10⁻¹² C²/N*m²

We can solve for E, as follows:

`E = (1)/(4*\pi*8.85e-12C2/N*m2 ) *(-16.2e-9C)/((2.8*0.295m)^(2)) =-0.21e3 N/C`

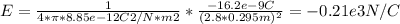
⇒ E = -0.21*10³ N/C

d) r= 7.30 R

In order to find the electric field at this distance, which falls beyond the outer radius of the shell, we need to find the total charge on the outer surface.

As the sphere has a charge of -16.2 nC, and the total charge of the conducting shell is 66.7nC, in order to make E=0 inside the shell, the total charge enclosed by a gaussian surface with a radius larger than the inner radius of the shell and shorter than the outer one, must be zero, which means that a charge of +16.2 nC must be distributed on the inner surface of the shell.

This leaves an excess charge on the outer surface of the shell as follows:

Qsh = 66.7 nC - 16.2 nC = 50.5 nC

Now, we can repeat the same process than for a) and c) as follows:

E*A = Q/ε₀, where Q= 50.5 nC, A= 4*π*(7.3R)² and ε₀ =8.85*10⁻¹² C²/N*m²

We can solve for E, as follows:

`E = (1)/(4*\pi*8.85e-12C2/N*m2 ) *(50.5e-9C)/((7.3*0.295m)^(2)) =0.1e3 N/C`

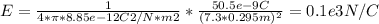
⇒ E = 0.1*10⁻³ N/C