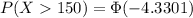Answer:
Explanation:
Let the random variable
 denote the time needed to train a contestant.
denote the time needed to train a contestant.
Suppose that the time it takes to train a contestant has mean 10 days and standard deviation 2 days, independent of the time it takes other contestants to train. Therefore,
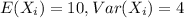
Let
 be a random variable that counts the number of days needed to train all candidates. Thus,
be a random variable that counts the number of days needed to train all candidates. Thus,
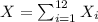
Then, by taking expectation of both sides, we obtain
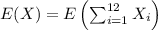
Because of the linearity of expectation, we obtain

It is given that for all
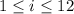
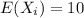
Now, we have that
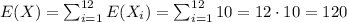
which means that the total time needed to train all candidates is 120 days.
Let's calculate the variance of
 . It is given that the time needed to train one candidate is independent of the time it takes other contestants to train. Hence, we know that
. It is given that the time needed to train one candidate is independent of the time it takes other contestants to train. Hence, we know that
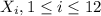 are independent. Therefore, the variance of a sum of 12 random variables equals the sum of variances of each of them and we obtain
are independent. Therefore, the variance of a sum of 12 random variables equals the sum of variances of each of them and we obtain
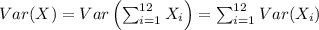
It is given that for all
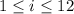
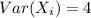
Now, we have that
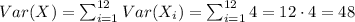
Apply the Central Limit Theorem.
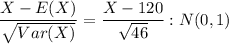
Now, let's calculate the probability that it will take more than 150 days to train all the contestants.
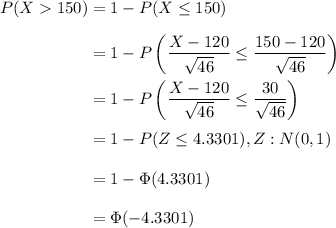
Therefore, the approximation by the Central Limit Theorem that it will take more than 150 days to train all the contestants is