Question

Find an explicit formula for the sequence given by the recursive definition v_n = 3v_n-1, v_1 = 45

​

Answer 1

Answer: Choice D
`\textrm{v}_n = 15(3^n)`

=====================================================

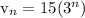
Work Shown:

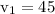`\textrm{v}_1 = 45` is the first term

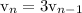`\textrm{v}_n = 3\textrm{v}_(n-1)` means we multiply the previous term (
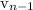`\textrm{v}_(n-1)`) by 3 to get the next term (
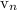`\textrm{v}_n`). Therefore, r = 3 is the common ratio. This sequence is geometric.

Let's find the explicit formula

`\textrm{v}_n = a*r^(n-1)`

`\textrm{v}_n = \textrm{v}_1*r^(n-1)`

`\textrm{v}_n = 45*3^(n-1)`

`\textrm{v}_n = 45*3^n*3^(-1)`

`\textrm{v}_n = 45*3^(-1)*3^n`

`\textrm{v}_n = \left(45*(1)/(3)\right)*(3^n)`

`\textrm{v}_n = 15(3^n)`

--------

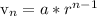
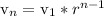
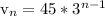
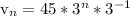
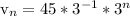
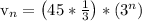
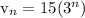
For each sequence mentioned, the starting term is at n = 1.

So to check our work, we can plug n = 1 into the equation we just found to get...

`\textrm{v}_n = 15*(3^n)`

`\textrm{v}_1 = 15*(3^1)`

`\textrm{v}_1 = 45`

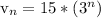
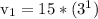
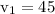
The other terms are generated in a similar fashion.