Question

A researcher wants to study sports-watching behavior of young men. In a random sample of 18 young adult men 20-30 years old, each person was asked how many minutes of sports he watched on TV daily. The researcher wishes to test whether the mean amount of television watched daily by young men is greater than 50 minutes.

What would be a Type I error, in the context of this problem?

a. The researcher concludes that the mean amount of television watched by young men is greater than 50, when the mean is really greater than 50.
b. The researcher concludes that the mean amount of television watched by young men is greater than 50, when the mean is really less than or equal to 50.
c. The researcher concludes that the true mean amount of television watched by young men is equal to 50, when the mean is really less than 50.
d. The researcher fails to conclude that the mean amount of television watched by young men is greater than 50, when the mean is really greater than 50.
e. The researcher concludes that the mean amount of television watched by young men is less than or equal to 50, when the mean is really less than or equal to 50.

Answer 1

Null hypothesis:
`\mu \leq 50`

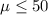
Alternative hypothesis:
`\mu >50`

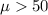
A type of error I for this case would be reject the null hypothesis that the population proportion is lower or equal than 50 when actually is true.

So then the best option for this case is:

b. The researcher concludes that the mean amount of television watched by young men is greater than 50 (reject the null hypothesis), when the mean is really less than or equal to 50.

Explanation:

Previous concepts

A hypothesis is defined as "a speculation or theory based on insufficient evidence that lends itself to further testing and experimentation. With further testing, a hypothesis can usually be proven true or false".

The null hypothesis is defined as "a hypothesis that says there is no statistical significance between the two variables in the hypothesis. It is the hypothesis that the researcher is trying to disprove".

The alternative hypothesis is "just the inverse, or opposite, of the null hypothesis. It is the hypothesis that researcher is trying to prove".

Type I error, also known as a “false positive” is the error of rejecting a null hypothesis when it is actually true. Can be interpreted as the error of no reject an alternative hypothesis when the results can be attributed not to the reality.

Type II error, also known as a "false negative" is the error of not rejecting a null hypothesis when the alternative hypothesis is the true. Can be interpreted as the error of failing to accept an alternative hypothesis when we don't have enough statistical power.

Solution to the problem

On this case we want to test if the mean amount of television watched daily by young men is greater than 50 minutes), so the system of hypothesis would be:

Null hypothesis:
`\mu \leq 50`

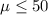
Alternative hypothesis:
`\mu >50`

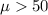
A type of error I for this case would be reject the null hypothesis that the population proportion is lower or equal than 50 when actually is true.

So then the best option for this case is:

b. The researcher concludes that the mean amount of television watched by young men is greater than 50 (reject the null hypothesis), when the mean is really less than or equal to 50.