Question

If 5% of all vehicles travel less than 39.15 m/h and 10% travel more than 73.23 m/h, what are the mean and standard deviation of vehicle speed

Answer 1

Standard deviation = 11.30 m/h

Mean = 57.74 m/h

Explanation:

Assume that the travel speed is normally distributed.

The corresponding z-score to the 5th and 90th percentile of normal distribution are, respectively, -1.645 and 1.282.

For any given speed X, the z-score is:

`z= (X-\mu)/(\sigma)`

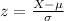
If z = -1.645 for X = 39.15 and z= 1.282 for X=72.23, the following system can be solved for the mean and standard deviation of vehicle speed:

`-1.645= (39.15-\mu)/(\sigma)\\1.282= (72.23-\mu)/(\sigma)\\\\-1.645 -1.282 = (39.15-72.23)/(\sigma) \\\sigma=11.30\ m/h\\\mu =72.23-(1.282*\sigma)\\\mu=57.74\ m/h`

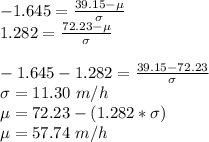
The standard deviation is 11.30 m/h and the mean is 57.74 m/h.