Answer:
a)
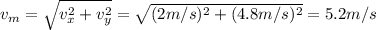
b)
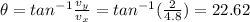 degrees and on this case to the South of the East.
degrees and on this case to the South of the East.
c)
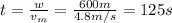
d)
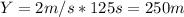
So it would be 250 to the South
Step-by-step explanation:
Part a
For this case the figure attached shows the illustration for the problem.
We know that
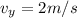 represent the velocity of the river to the south.
represent the velocity of the river to the south.
We have the velocity of the motorboard relative to the water and on this case is
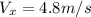
And we want to find the velocity of the motord board relative to the Earth
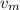
And we can find this velocity from the Pythagorean Theorem.
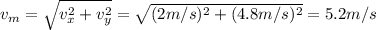
Part b
We can find the direction with the following formula:
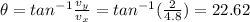 degrees and on this case to the South of the East.
degrees and on this case to the South of the East.
Part c
For this case we can use the following definition
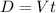
The distance would be D = w = 600 m and the velocity V = 4.8m/s and if we solve for t we got:
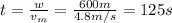
Part d
For this case we can use the same definition but now using the y compnent we have:
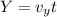
And replacing we got:
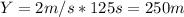
So it would be 250 to the South