Answer:
See proofs below
Explanation:
a) Consider the sequence {an}={(-1)^n}={-1,1,-1,1,...}
an has an infinite number of ones. Indeed, if n is even, (-1)^n=1, and there are infinite even numbers, hence infinite ones. However, {an} does not converge to one, because {an} is divergent (it oscillates between 1 and -1).
b) This is impossible. We will use the definition of limit to see why.
Let
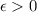 . Suppose that {an} has an infinite number of ones, and suppose that {an} converges to L. Then, there exists some M>0 such that if n≥M then
. Suppose that {an} has an infinite number of ones, and suppose that {an} converges to L. Then, there exists some M>0 such that if n≥M then
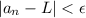 . Now, there exist infinite natural numbers n≥M such that an=1 by hypotheses. Then
. Now, there exist infinite natural numbers n≥M such that an=1 by hypotheses. Then
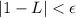
Hence L and 1 get arbitrarily close, therefore L=1.
c) It is possible to construct such a sequence:
{an}={1,0,1,1,0,1,1,1,0,1,1,1,1,0,1,1,1,1,1,0,1,1,1,1,1,1,0,...}
even if there is not a simple explicit formula. The sequence is divergent because it has infinite zeroes and infinite ones (thus L should be either 0 or 1, but it can't be both).