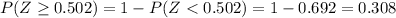Question

George Washington was 6 feet tall. Find the z-score for George Washington. Find the probability that a randomly selected individual will be as tall or taller than George Washington. Interpret both the z-score and the probability in a sentence. Hint: change feet into inches first. It is easiest to calculate the z-score by hand (look back to chapter 7).

Answer 1

`P(X\geq 6)=P((X-\mu)/(\sigma)\geq (6-\mu)/(\sigma))=P(Z\geq (6-5.833)/(0.333))=P(Z\geq 0.502)`

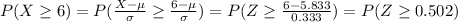
And we can find this probability using the complement rule:

`P(Z\geq 0.502)=1-P(Z<0.502)`

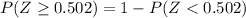
And in order to find these probabilities we can find tables for the normal standard distribution, excel or a calculator.

`P(Z\geq 0.502)=1-P(Z<0.502)=1-0.692=0.308`

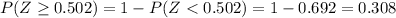
Explanation:

Assuming this complete question "It will be necessary to know that the average height for men is assumed to be 70 inches with a standard deviation of 4 inches. To receive full credit, you also need to comment on two other posts from your classmates (you can just state whether or not you agree with their solution and if not, what you did differently).

George Washington was 6 feet tall. Find the z-score for George Washington. Find the probability that a randomly selected individual will be as tall or taller than George Washington. Interpret both the z-score and the probability in a sentence. Hint: change feet into inches first. It is easiest to calculate the z-score by hand (look back to chapter 7)."

Previous concepts

Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".

The Z-score is "a numerical measurement used in statistics of a value's relationship to the mean (average) of a group of values, measured in terms of standard deviations from the mean".

Solution to the problem

Let X the random variable that represent the heights of a population, and for this case we know the distribution for X is given by:

`X \sim N(70,4)`

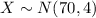
Where
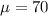`\mu=70` and
`\sigma=4`

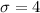
If we convert this into feet we got:

`70 in*(1ft)/(12 in)= 5.83 ft`

`4 in*(1ft)/(12 in)= 0.333 ft`

`X \sim N(5.83,0.333)`

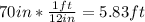
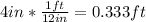
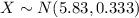
We are interested on this probability

`P(X\geq 6ft)`

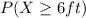
And the best way to solve this problem is using the normal standard distribution and the z score given by:

`z=(x-\mu)/(\sigma)`

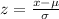
If we apply this formula to our probability we got this:

`P(X\geq 6)=P((X-\mu)/(\sigma)\geq (6-\mu)/(\sigma))=P(Z\geq (6-5.833)/(0.333))=P(Z\geq 0.502)`

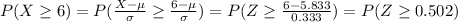
And we can find this probability using the complement rule:

`P(Z\geq 0.502)=1-P(Z<0.502)`

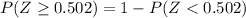
And in order to find these probabilities we can find tables for the normal standard distribution, excel or a calculator.

`P(Z\geq 0.502)=1-P(Z<0.502)=1-0.692=0.308`