Question

A. A researcher reads that in the population of US students, the average income of students is $1500. In a random sample of 300 students, he finds that the mean monthly income is $1,445 with a standard deviation of $530. Conduct a one-tailed t-test to see if the mean in his sample is significantly (p<.05) lower than the population mean. What is the value of "t" that you find?

B. In the previous question, there were 300 respondents. Look at the t-test table in your book. If the t-score that was calculated was between 1.7 and 1.9, would you be able to reject the null hypothesis (p<.05) that the means of the sample and the population are the same? [Note: Because we have a prediction (that the sample might be less than the population) we use a one-tailed test.]

c. In the previous example, could you reject the null hypothesis with 99% confidence?

Answer 1

A. Value of t = -1.7974 .

B. If the t-score that was calculated was between 1.7 and 1.9, we will not be able to reject the null hypothesis.

C. No, we can't reject the null hypothesis with 99% confidence.

Explanation:

We are given the population mean income of students,
`\mu` = $1500.

Let, Null Hypothesis,
`H_0` :
`\mu` = $1500

Alternate Hypothesis,
`H_1` :
`\mu` < $1500

A. The one-tailed t statistics used here is ;

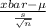`(xbar - \mu)/((s)/(√(n) ) )` follows
`t_n_-_1` where, xbar = sample mean = $1445

s = sample standard deviation = $530

n = sample size = 300

Test Statistics =
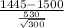`(1445 - 1500)/((530)/(√(300) ) )` follows
`t_2_9_9`

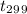
Value of t = -1.7974

Now, at 5% level of significance the t table will give a critical value of -1.9696. Since our test statistics is greater than critical value as -1.7974 > -1.9696 so we have insufficient evidence to reject null hypothesis and conclude that population mean is $1500 and sample mean is less than the population mean.

B. If the t-score that was calculated above was between 1.7 and 1.9 then also we haven't rejected the null hypothesis as then also our test statistics doesn't lie in the rejection region as 1.7 to 1.9 is greater than -1.9696. And we conclude that sample and the population mean are not same.

C. 99% Confidence Interval for
`\mu` =
`[xbar - 1.9696*(s)/(√(n) ) , xbar + 1.9696*(s)/(√(n) )]`

=
`[1445 - 1.9696*(530)/(√(300) ) , 1445 + 1.9696*(530)/(√(300) )]`

= [ 1384.731 , 1505.269 ]

Since, $1500 lies in this 99% confidence interval so still we can't reject null hypothesis.