Question

Please hurry. Solve the equation

Answer 1

The value of x is
`5\sqrt[3]{25}`.

Solution:

Given expression is
`-7=8-3 \sqrt[5]{x^(3)}`.

Switch both sides.

`8-3 \sqrt[5]{x^(3)}=-7`

Subtract 8 from both side of the equation.

`8-3 \sqrt[5]{x^(3)}-8=-7-8`

`-3 \sqrt[5]{x^(3)}=-15`

Divide by –3 on both side of the equation.

`$\frac{-3 \sqrt[5]{x^(3)}}{-3} =(-15)/(-3)`

`\sqrt[5]{x^(3)}=-5`

To cancel the cube root, raise the power 5 on both sides.

`(\sqrt[5]{x^(3)})^5=(-5)^5`

`x^3=3125`

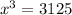
To find the value of x, take square root on both sides.

`\sqrt[3]{x^3}=\sqrt[3]{25}`

`x=5\sqrt[3]{25}`

Hence the value of x is
`5\sqrt[3]{25}`.