Answer:
3696508354.42 $
Explanation:
P= 2000$
No of terms per year = 4
==> number of terms for the period= 4×20=80
Quarterly interest rate = 8
so yearly rate = 8/3×12=48%
We know formula for compound interest is;
A= P
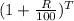
Where,
A= amount required
P = principal or invested amount
R = rate of interest per year
T = number of terms for the period
Putting values
==> A =
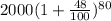
==> A= 2000
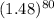
==> A = 2000(4.1776998×442409.523348)
==> A= 2000×1848254.17721
==> A= 3696508354.42 $