Question

Two particles, A and B, are in uniform circular motion about a common center. The acceleration of particle A is 4.9 times that of particle B. The period of particle B is 2.4 times the period of particle A. The ratio of the radius of the motion of particle A to that of particle B is closest to________.

Answer 1

`(R_A)/(R_B)=0.85`

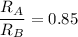
Step-by-step explanation:

given,

Acceleration of Particle A = 4.9 times particle B

Period of particle B = 2.4 times Period of A

Ratio of radius of the motion of particle A to B = ?

For Particle A

`a_A = (v_A^2)/(R_A)`

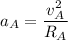
For Particle B

`a_B = (v_B^2)/(R_B)`

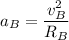
Form the question

`(a_A)/(a_B)=4.9`

`(v_A^2R_B)/(v_B^2R_A)=4.9`

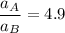
and

`(T_B)/(T_A)=2.4=(R_Bv_A)/(v_BR_A)`

`5.76 = (R_B^2v_A^2)/(v_B^2R_A^2)`

`5.76= 4.9* (R_B)/(R_A)`

`(R_A)/(R_B)=0.85`

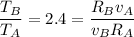
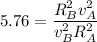
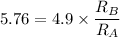
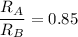
Hence, the ration of the radius of the Particle A that of B = 0.85.