Question

The village of Hempstead has been taking a look at the issue of responding to 911 calls. It is a small community and geographically dispersed, so the response calls have been relatively slow. The following is the response rates for the last five calls: 17 minutes, 12 minutes, 9 minutes, 16 minutes, and 14 minutes.

What was the mean response time for 911 calls in this village?

a. 13.6 minutes
b. 12.6 minutes
c. 14.2 minutes
d. 10.2 minutes

Answer 1

`\bar X = (17+12+9+16+14)/(5)= 13.6min`

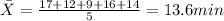
So then the best answer for this case would be:

a. 13.6 minutes

Step-by-step explanation:

For this case we have the following data for the response rates:

17,12,9,16,14

And we want to calculate the mean response time for 911 calls in this village.

And for this case we use we can use the definition of sample mean given by:

`\bar X = (\sum_(i=1)^n X_i)/(n)`

Where n = 5 represent the sample size for this case. If we replace we got:

`\bar X = (17+12+9+16+14)/(5)= 13.6min`

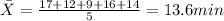
So then the best answer for this case would be:

a. 13.6 minutes

The sample mean is an estimator unbiased of the population mean because:

`E(\bar X) = E((\sum_(i=1)^n X_i)/(n)) = (1)/(n) \sum_(i=1)^n E(X_i) = (n\mu)/(n)= \mu`

For this reason is a good statistic if we want to see central tendency in a group of values.