Question

A fireman standing on a 9.1 m high ladder operates a water hose with a round nozzle of diameter 1.8 inch. The lower end of the hose (9.1 m below the nozzle) is connected to the pump outlet of diameter 3.1 inch. The gauge pressure of the water at the pump is(gauge) Plamp-P,tin 50.6 PSI 348.875 kPa (abs) pump atmCalculate the speed of the water jet emerging from the nozzle. Assume that water is an incompressible liquid of density 1000 kg/m^3 and negligible viscosity. The acceleration of gravity is 9.8 m/s^2 . Answer in units of m/s.

Answer 1

The speed of the water jet emerging from the nozzle is 24.21 m/s.

Step-by-step explanation:

Given that,

Height = 9.1 m

Diameter =1.8 inch

Gauge pressure = 348.875 kPa

We need to calculate the speed of the water jet emerging from the nozzle

Using Bernoulli's equation

`(1)/(2)\rho(v_(n)^2-v_(p)^2)=P_(gauge)-\rho gh`

`(v_(n)^2-v_(p)^2)=((2)/(\rho))P_(gauge)-2gh`

`v_(n)^2-((A_(n))/(A_(p)))^2v_(n)^2=((2)/(\rho))P_(gauge)-2gh`

`v_(n)^2-((r_(n))/(r_(p)))^4v_(n)^2=((2)/(\rho))P_(gauge)-2gh`

`v_(n)^2=(((2)/(\rho))P_(gauge)-2gh)/(1-((r_(n))/(r_(p)))^4)`

`v_(n)=\sqrt{(((2)/(\rho))P_(gauge)-2gh)/(1-((r_(n))/(r_(p)))^4)}`

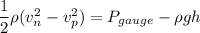
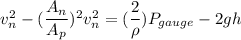
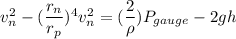
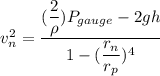
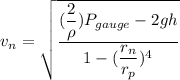
Put the value into the formula

`v_(n)=\sqrt{((2)/(1000)*348.875*10^(3)-2*9.8*9.1)/(1-((0.9)^4)/((1.55)^4))}`

`v_(n)=24.21\ m/s`

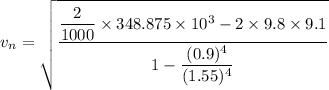
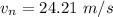
Hence, The speed of the water jet emerging from the nozzle is 24.21 m/s.