Question

Wire A has the same length and twice the radius of wire B. Both wires are made of the same material and carry the same current. Which of the following equations is true concerning the drift velocities vA and vB of electrons in the wires?a. vA = vB/4b. vA = vB/2c. vA = 4vBd. vA = vBe. vA = 2vB

Answer 1

`V_A= (I_A)/(n_A e A_A)= (I)/(ne 4A_B)= (1)/(4) (I)/(neA_B)`

`V_B= (I_B)/(n_B e A_B)= (I)/(ne A_B)`

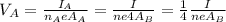
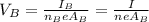
And as we can see we have that:

`V_A = (1)/(4) V_B`

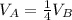
So then the best answer would be:

a. vA = vB/4

Step-by-step explanation:

For this case we know the following conditions:

`L_A = L_B =L` same length

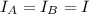`I_A = I_B =I` both wires with the same current

Both wires are made of he same material, so then the number of electrons per cubic meter (n) are the same for both wires
`n_A = n_B =n`

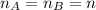
We also know that
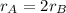`r_A = 2 r_B` where r represent the radius.

Since we know that a wire have a cylindrical form we can find the area for each case:

`A_A= \pi r^2_A = \pi (2r_B)^2 = 4 \pi r^2_B= 4 A_B`

`A_B = \pi r^2_B`

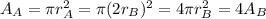
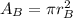
So then we have that
`A_A = 4 A_B`

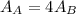
Now we know that from the definition the drift velocity of electron in a wire is given by:

`v_d = (I)/(neA)`

Where I is the current, n the number of electrons per cubic meter, e is the charge for the electron and A the area.

If we replace we have this:

`V_A= (I_A)/(n_A e A_A)= (I)/(ne 4A_B)= (1)/(4) (I)/(neA_B)`

`V_B= (I_B)/(n_B e A_B)= (I)/(ne A_B)`

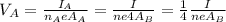
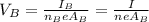
And as we can see we have that:

`V_A = (1)/(4) V_B`

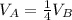
So then the best answer would be:

a. vA = vB/4