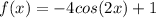Question

Help ASAP!!
Using the graphed function above, find the following

Answer 1

Maximum: 1, Minimum: -3, Midline y = -1, Amplitude = 4, Period =
`\pi`, Frequency
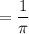`\displaystyle =(1)/(\pi)`, equation :
`f(x)=-4cos(2x)+1`

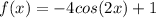
Explanation:

Sinusoid Functions

It refers to the oscillating functions like the sine or cosine which range from a minimum and maximum value periodically.

The graph shown can give us all the information we need to answer these questions:

Maximum: 1

Minimum: -3

The midline goes through the center value (mean) of the max and min values, i.e.

Equation of the midline:

`\displaystyle y=(1-3)/(2)=-1`

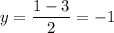
Amplitude is the difference between the maximum and minimum values

`A=1-(-3)=4`

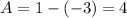
The period is the time it takes to complete a cycle. We can see the minimum value is first reached at x=0 and next at
`x=\pi`

Thus the period is

`T=\pi`

The frequency is the reciprocal of the period:

`\displaystyle f=(1)/(T)=(1)/(\pi)`

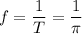
The angular frequency is

`\displaystyle w=2\pi f=(2\pi )/(\pi)=2`

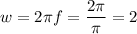
The equation of the function is a negative cosine (since it starts at the minimum) or a shifted sine or cosine. We'll choose the negative cosine, knowing all the parameters:

`f(x)=-4cos(2x)+1`