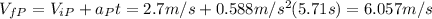Question

Mark and Paul are in a race. Mark is 20 meters from the finish line and running at a constant 3.5 m/s. Paul is 5 meters behind him and running at 2.7 m/s, but he is accelerating with a constant acceleration. At what rate must Paul accelerate to tie the race?

Answer 1

`25 m= 2.7 m/s * (5.71 s)+ (1)/(2) a (5.71s)^2`

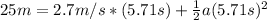
And solving for a we got:

`9.583 m = (1)/(2) a (5.71s)^2`

`a = 0.588 (m)/(s^2)`

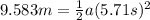
Step-by-step explanation:

For this case we have an illustration for the problem on the figure attached.

And we can solve this problem analyzing each one of the runner. Let's begin with Mark

Mark

For this case we know that
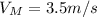`V_M = 3.5 m/s` and th velocity is constant. The distance from Mark and the finish line is
`D_M = 20 m`

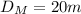
Since the velocity is constant we can create the following relation:

`D_M = V_M t_M`

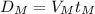
And solving for
`t_M` we got:

`t_m = (D_M)/(V_M)= (20m)/(3.5 m/s)= 5.71 s`

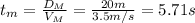
So then Mark will nd the race after 5.71 seconds

Paul

We know that the initial velocity for Paul is given
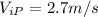`V_(iP)= 2.7 m/s` we also know that the total distance between Paul and the finish line is 25 m and we want to find the acceleration that Paul needs to apply in order to tie the race, and Paul have 5.71 sconds in order to reach the finish line.

We can use this formula in order to find the acceleration (because we assume that the acceleration is constant) that he needs to apply:

`x_f = x_i + v_i t + (1)/(2) a t^2`

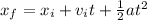
And since
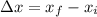`\Delta x = x_f - x_i` we have this:

`\Delta x= v_i t + (1)/(2) a t^2`

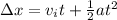
And if we replace we have this:

`25 m= 2.7 m/s * (5.71 s)+ (1)/(2) a (5.71s)^2`

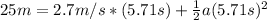
And solving for a we got:

`9.583 m = (1)/(2) a (5.71s)^2`

`a = 0.588 (m)/(s^2)`

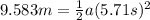
And the final velocity for Paul using this acceleration would be:

`V_(fP)= V_(iP)+ a_P t = 2.7m/s + 0.588 m/s^2 (5.71s)= 6.057 m/s`