Question

Shankar is teaching 2 courses, let us call them 435 and FYS. 435 has 3 sophomores, 8 juniors and 13 seniors; FYS has 5 sophomores, 7 juniors and 6 seniors. Suppose he wants to understand how his teaching is for the students. He picks one student from each class at random. Find the probability that both students are of the same type (i.e. both sophomores, or both juniors etc). Simplify your answer so it looks like a fraction without any factorials.

Answer 1

The probability that both students are of the same type is
`(149)/(432)`.

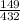Explanation:

The students in 435 are: {3 sophomores, 8 juniors and 13 seniors}

Number of students in 435 = 3 + 8 + 13 = 24

The students in FYS are: {5 sophomores, 7 juniors and 6 seniors}.

Number of students in FYS = 5 + 7 + 6 = 18

The teacher picks 1 student from each class.

The probability that both students are of the same type is:

P (Same type students) = P (Both are Sophomores) + P (Both are Juniors)

+ P (Both are Seniors)

= P (Sophomore ∩ Course 435) × P (Sophomore ∩ Course FYS)

+ P (Junior ∩ Course 435) × P (Junior ∩ Course FYS)

+ P (Senior ∩ Course 435) × P (Senior ∩ Course FYS)

`=[((3)/(24) )*((5)/(18))]+[((8)/(24) )*((7)/(18))]+[((13)/(24) )*((6)/(18))]\\=(15+56+78)/(432)\\ =(149)/(432)`

Thus, the probability that both students are of the same type is
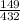`(149)/(432)`.