Question

As relay runner A enters the 65-ft-long exchange zone with a speed of 30 ft/s, he begins to slow down. He hands the baton to runner B 2.5 s later as they leave the exchange zone with the same velocity. Determine (a) the uniform acceleration of each of the runners, (b) when runner B should begin to ru

Answer 1

a)
`a_A = (2* (-10ft))/((2.5s)^2)= -3.2 (ft)/(s^2)`

`a_B = (V^2_(fB) -V^2_(iB))/(2 \Delta x)= ((22ft/s)^2 -(0))/(2*65 ft)= 3.72 (ft)/(s^2)`

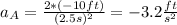
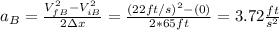
b) For this case we can use this formula:

`t= (V_f - V_i)/(a)`

And replacinf for the runner B we got:

`t= (22 ft/s -0 ft/s)/(3.72 ft/s^2)= 5.91 s`

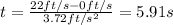
And the runner B should begin to run at:

`t_(B start)= 5.91-2.5 s = 3.41 sec`

Step-by-step explanation:

For this case we have the following info given:

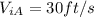`V_(iA)= 30 ft/s` represent the initial velocity for runner A

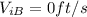`V_(iB)= 0 ft/s` represent the initial velocity for runner B

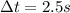`\Delta t = 2.5 s` represent the difference of time between the two runners

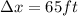`\Delta x= 65 ft` represent the total distance for the exchange zone.

Part a

For this case we can use the following formula:

`x_f = x_i + v_i t +(1)/(2)at^2`

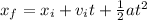
And we can define
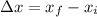`\Delta x = x_f -x_i` and we can convert this equation into:

`\Delta x= v_i t +(1)/(2)at^2`

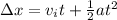
And we can find the acceleration since we have all the other values like this:

`65 ft = 30(ft)/(s) (2.5s) + (1)/(2)a_A (2.5s)^2`

`-10 ft =(1)/(2)a_A (2.5s)^2`

`a_A = (2* (-10ft))/((2.5s)^2)= -3.2 (ft)/(s^2)`

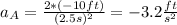
And that would be the acceeleration for the runner A.

For the acceleration of the runner A we need to take in count that
`V_(fA)= V_(fB)`

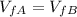
And for this case we can use this:

`V_(fB)= V_(fA)= V_(iA)+ a_A t`

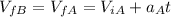
And if we replace we got:

`V_(fB)= V_(fA)= 30 (ft)/(s)+ (-3.2 (ft)/(s^2)) (2.5s) = 22 (ft)/(s)`

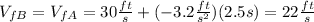
So for this case we have
`V_(iB)= 0ft/s , V_(fB)= 22 ft/s, \Delta x= 65 ft`, and we can use this formula:

`V^2_f = V^2_i + 2 a \Delta x`

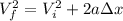
And solving for a we got:

`a_B = (V^2_(fB) -V^2_(iB))/(2 \Delta x)= ((22ft/s)^2 -(0))/(2*65 ft)= 3.72 (ft)/(s^2)`

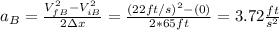
Part b

For this case we can use this formula:

`t= (V_f - V_i)/(a)`

And replacinf for the runner B we got:

`t= (22 ft/s -0 ft/s)/(3.72 ft/s^2)= 5.91 s`

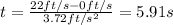
And the runner B should begin to run at:

`t_(B start)= 5.91-2.5 s = 3.41 sec`