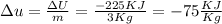Answer:
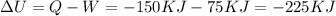
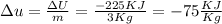
Step-by-step explanation:
For this case we know the mass of the system
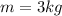
For this case the work done by the system is +75 KJ and is positive since we assume that the work is done on the sytem by the surroundings
And the heat for this case would be negative since is transferred from the system to the sorroundings Q = -150 KJ
From the problem we know that the can neglect the potential and the kinetic energy so then we have that:

Using the first law of thermodynamics we know this:
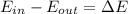
Where E means energy, and if we replace we have:
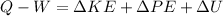
So then we have just this formula:
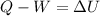
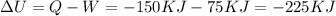
And then since we need the specific internal energy we can do this: