Answer:
One mole of an ideal gas is contained in a cylinder with a movable piston. The temperature is constant at 77 °C. Weights are removed suddenly from the piston to give the following sequence of three pressures.
a. P1 = 5.50 atm (initial state)
b. P2 = 2.43 atm
c. P3 = 1.00 atm (final state)
What is the total work (in joules) in going from the initial to the final state by way of the preceding two steps?
The answer to the question is
The total work (in joules) in going from the initial to the final state by way of the preceding two steps is equal to -4685.6 Joules
Step-by-step explanation:
For a constant temperature or isothermal process, we have
P₁V₁ = P₂V₂ = P₃V₃ which gives
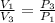
From the first law of thermodynamics, Q =ΔU+W and ΔU = 0 therefore
Q = W and the work done is given by Q = n·R·T·
=
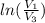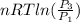
Where
T = 77 °C = 350.15 K
P₁ = 5.00 atm
P₂ = 2.24 atm
P₃ = 1.00 atm
n = 1 mole
R = 8.3145 J/mol·K
We are required to find the the total work (in joules) in going from the initial to the final state by way of the preceding two steps
Therefore we have
Total work done is given by
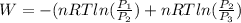or
Which by the logarithm laws ㏑(A)+㏑(B) = ㏑(A×B) the equation becomes
=
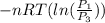therefore the equation is the same for calculating directly from the initial pressure P₁, to the final pressure P₃
Therefore W = (1.00 mol)×(8.3145 J/mol·K)×
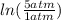
= -4685.6 J or -4.69 kJ
The total work (in joules) in going from the initial to the final state by way of the preceding two steps is the same as the work arrived at by calculating directly from the initial to the final state bypassing the intermediate state, P₂ and is equal to -4685.6 Joules. This is so because P₁V₁ = P₂V₂ = P₃V₃